Primitive Hierarchical Processes and the Structure of a Single Note
Decades after its publication, Lerdahl and Jackendoff's Generative Theory of Tonal Music remains more-or-less unrivaled as a thorough and coherent account of how humans arrive at hierarchically-organized interpretations of sounding music. One of the features of the theory that makes it so successful is its careful organization in layers or phases which must be considered in turn -- in the original model these were grouping, meter, time-span reduction and prolongational reduction. Subdividing the overall problem into these discrete topics allows one to focus on very specific details while remaining confident of the big picture, and the overall theory is one that carries a listener from very early and relatively simple stages of perception to the kind of sophisticated event-hierarchical interpretations that mainstream theorists like to talk about. It is this totalizing impulse that makes the work valuable.
In GTTM the authors were careful to note that their theory was not a model of real-time processing, but rather a means of predicting the "final state" of perception. In subsequent writings, however, both authors have suggested that the partitioning of grouping, meter, and event hierarchy reflects an actual cognitive ordering. [1]
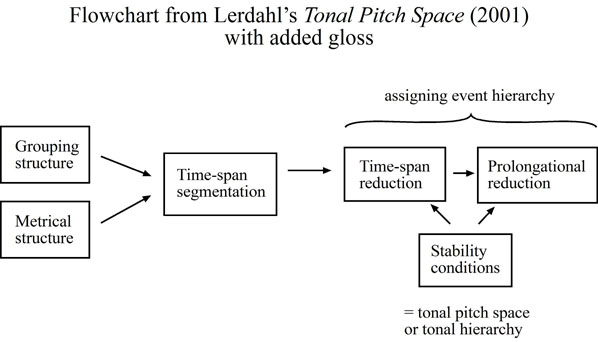
Here I've reproduced Lerdahl's diagram from the beginning of Tonal Pitch Space. The text outside the boxes is my own added gloss - Lerdahl explains that he thinks the last two boxes are basically the same process approached from different perspectives. These are your "inner Schenkerian," if you will, which organize the sounding music into what music psychologists would call an event hierarchy.
As an actual cognitive structure, the GTTM theory is problematic. It is complex - it evokes multiple discrete and fully coherent structures for a single stimulus. It is too music-specific, focusing on the problems of music analysts without relating the model to other kinds of everyday hearing. Finally, it is not dynamic and cannot easily be made dynamic - each phase requires a large amount of input to make determinations, and there is little sense of how perception behaves on the way to the final state. [2]
In this paper I begin the process of dismantling and reconfiguring Lerdahl and Jackendoff's cognitive flowchart into a model that is simpler, less music-specific, and more dynamic. My strategy is to consider the perception of individual notes (and, more generally, individual sonic events), a phenomenon that the authors simply took as given. In going further back to the beginnings of aural perception a new sequence of priorities becomes clear. In particular, I assert that event-hierarchical organization, a process that the GTTM theory saves for the final stages, is actually present and highly influential early in the chain of events.
We can start with grouping. Now, the very idea of "grouping" suggests the combination of multiple entities into larger wholes, and the authors first preference rule strongly discourages construing a single event as a group. However, these Gestaltist principles are, in part, a recursion of the processes that define single events. Both levels are concerned with two essential phenomena - "edge-finding" and "continuity."
The two properties go hand in hand. "Edges" or "boundaries" alert us to the beginnings of important events. That which lies between boundaries is judged to be continuous. A typical musical sound begins with a relatively sudden attack as an initial edge, followed by a decay. We tend to be less interested in the actual cessation of the sound - instead there is a sense that the event continues until the next attack. In the typical musical sound there is no real terminal edge.
This makes good ecological sense. Attacks correspond to the greatest expenditure of energy in our sound source - they are "the important part" of the event that we would have an interest in tracking. Gradual decays are indeterminate - the sound may still be continuing but we just can't hear it - and these decays simply do not correspond to important events.
Lerdahl and Jackendoff's larger-scale groupings function the same way - the grouping slurs begin at prominent boundaries and engulf any silence that might follow. It is a recursion of the same basic shape.
Lerdahl and Jackendoff's Grouping Preference Rule #3
GPR 3 (Change)Consider a sequence of four notes n1n2n3n4. All else being equal, the transition n2-n3 may be heard as a group boundary if
b. (Dynamics) the transition n2-n3 involves a change in dynamics and n1-n2 and n3-n4 do not, or if
c. (Articulation) the transition n2-n3 involves a change in articulation and n1-n2 and n3-n4 do not, or if
d. (Length) n2 and n3 are of different lengths and both pairs n1,n2 and n3,n4 do not differ in length.
Of all the Lerdahl and Jackendoff Grouping Preference Rules, GPR 3 in particular is involved in monitoring continuity in the sound signal, looking for points of transition that are particularly disjunct. 3c and d involve multi-event patterning, but a and b monitor properties that also define single events, namely pitch and amplitude. The following clips manipulate these properties to create simple boundaries.
To this list of boundary-defining properties we could probably also add timbre and spatial location.
Thus we can posit a cognitive faculty that monitors the sound signal for discontinuities, the detection of which marks the beginning of discrete events. Edge-detection would seem to be an extremely early stage in the process of aural perception, since it is necessary for the definition of sonic objects.
Now that we've got some idea of immediate, bottom-up factors that contribute to edge-finding, it is time to consider the other side of this concept, which is "continuity." In a Lerdahl and Jackendoff analysis, the grouping phase creates a layering of hierarchically-stacked slurs.
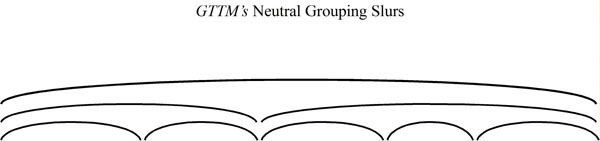
The content within these slurs is, for the time being, neutral - it is up to later phases of analysis to determine what they call the "head" of the group. I would like to suggest that this neutral encoding may not exist, as we don't seem to have much use for it. The sound signal is, after all, constantly in flux. Everything we hear is either the beginning of a new sound or the continuation of something that has already begun. In order to perceive continuity of events, we must be knitting each perceivable moment into an event hierarchy. Such a hierarchy could be described with Lerdahl and Jackendoff's branching symbols.
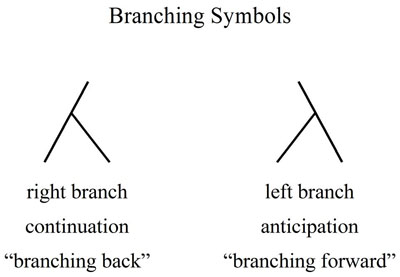
A right branch represents continuation, moving away from something that is hierarchically superordinate, and a left branching represents anticipation. As sounds unfold, we can assign a provisional hierarchical encoding on the fly.
Let us consider a few sounds that have an interesting hierarchical structure. So far I've been talking about attacks as though they are hard edges which occur instantaneously. However, this is not always the case. The world also creates many sounds that begin with a gentle upward slope of increasing amplitude. The actual attack of such a sound is assigned to the peak of this ascent. With an otherwise featureless stimulus, we can create a simple branching that follows amplitude -- as it rises, we branch forward, and as it falls we branch back. The attack, which is the most important part of the sound and the moment we feel that it essentially occurs, is the hierarchical center of the event.
We might be tempted to think that branching according to amplitude is actually sufficient for edge finding at this micro level. However, I think we still need a mechanism that is sensitive to other kinds of discontinuity like pitch and timbre which will act as an interrupt for branching. For instance, one phenomenon which this can't account for is the sudden drop-offs in amplitude that we heard earlier, which seem to read as new events.
In looking at the structure of individual notes, we are seeing the influence of low-level hierarchical processes that will shape the more sophisticated interpretations of later phases. Meter, in particular, is dependent on this encoding as it tracks events from attack to attack.
Herein lies our most aggressive revision of the Lerdahl and Jackendoff theory. (The flowchart from earlier is repeated below for your convenience.)

GTTM considers meter to be an input to event hierarchy. Their metric grid is, of course, a hierarchy in itself which alternates strong and weak elements. However, by speaking of it as a discrete domain that somehow precedes the real business of determining musical structure, they imply that it is essentially different in kind from event hierarchy.
I argue that many of the processes that determine event hierarchy are more likely to precede meter in the chain of cognitive events. They are, in fact, the means by which the metric sense interprets the signal and assigns a pattern of strong and weak beats. Thus, I refer to meter as post-hierarchical, and the processes that precede meter are pre-metric. Any property that has an influence on meter and can be observed in a non-metric stimulus is plausibly pre-metric.
Lerdahl and Jackendoff's Metric Preference Rule #4
Prefer a metrical structure in which beats of level Li that are stressed are strong beats of Li.
The authors' Metric Preference Rule 4 refers to local peaks in amplitude, which they call stress. Just as we saw the influence of this property in organizing single notes, we can also create non-metric, multi-event stimuli which exploit amplitude to create a hierarchy.
Perhaps we should think of this kind of stimulus as the normal state of affairs - the vast majority of sounds in the environment are, after all, not metered. Meter could be an evolutionary overlay on a preexisting means of sonic organization.
GTTM features analytic examples that consider every subdivision in a passage as a possible beat. This approach implies a similar cognitive mechanism of scanning a stimulus in order to find the best fit for a regular metric grid.
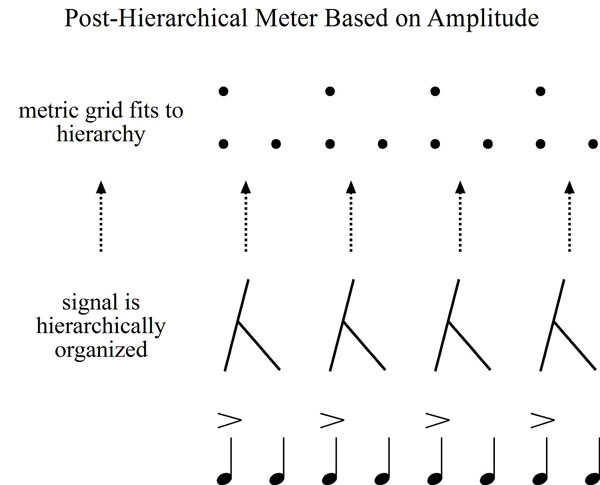
Conceiving of meter as post-hierarchical seems much more direct and efficient. Rather than scanning and evaluating possible beat positions, the metric facility could receive organized information and proceed from there. Thus, presented with a regular stimulus that alternates loud and soft, the metric system could simply latch on to what is presented post-hierarchically.
Metric Preference Rule #5 (Length)
Prefer a metrical structure in which a relatively strong beat occurs at the inception of either
b. a relatively long duration of a dynamic,
c. a relatively long slur,
d. a relatively long pattern of articulation,
e. a relatively long duration of a pitch in the relevant levels of the time-span reduction, or
f. a relatively long duration of a harmony in the relevant levels of the time-span reduction (harmonic rhythm).
Metric Preference Rule 5 cites the influence of the agogic accent, which privileges events that are relatively long. This is another force that we can observe in a non-metric stimulus.
Again, we can imagine that if the metric facility were presented with a recurring pattern of long and short, it would probably receive the long notes as the most likely position to place a beat, rather than testing every possible subdivision.
At this point one probably wants to protest. What about syncopation and cross rhythms? Musical stimuli are rarely this simple. This is true - actual rhythmic experience involves some tension between sounding rhythms and an underlying pulse. The accents of the musical surface are in a feedback loop with meter.
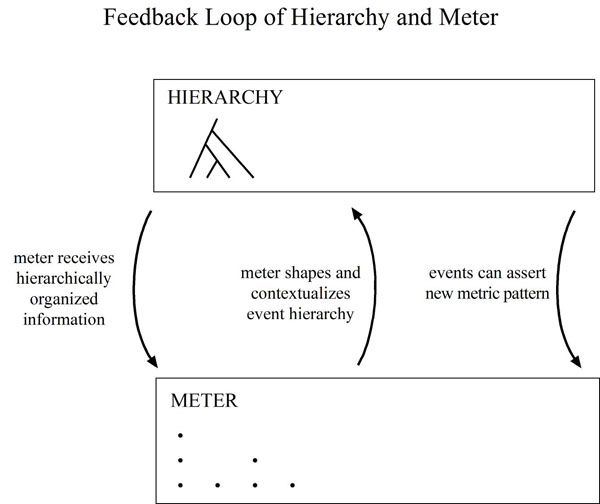
First, the metric context is defined by surface events organized hierarchically. Sounding figurations are then strongly characterized by their metrical context, but an incompatible structure can disrupt and redefine that context.
In order to understand this interaction, we need to look more closely at what meter is and how it works, and we'll use Christopher Hasty's model from Meter as Rhythm. The basic mechanism is the projective metric span. Given two sounding events, we have the ability to estimate a third point in the future that replicates the same time span.
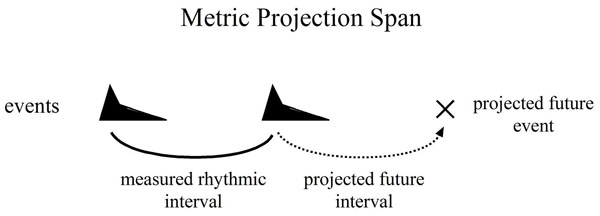
Meter is thought to be a chain of these projected spans.
What's interesting about these projected events is that they often feel real and palpable, even if nothing sounds at the predicted moment. It is as if one can see the next pulse coming over the horizon - at any given point one knows how far away it is, and we can interact with the moment with precision, tapping a foot, performing a note, or merely observing it consciously as it passes. However, we can really only anticipate one beat ahead.
I argue that projected beats are similar in kind to sounding events. They are silent events in and of themselves. Syncopated sounds interact with beats in the same kind of event hierarchy that we apply to notes.
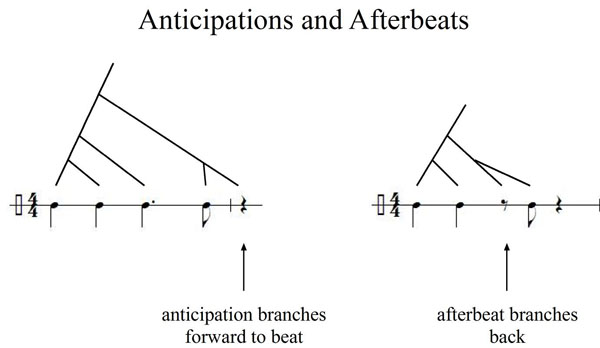
An anticipatory syncopation branches forward to the beat it preempts - there is a sense that the sounding event "belongs" to that silent beat. An afterbeat would similarly branch backwards.
What sounds during a projected metric interval also tends to "belong" to that interval as a subdivision. We expect subdivisions to be in rational intervals of 2 and 3, which create subpulses that can also project their own spans, and in most Western music this is indeed the case. This layered construction is what allows Lerdahl and Jackendoff to posit a well-formed and coherent metric grid that conforms to rules.
However, subdivisions need not be rational and projective, and the effect of non-projective divisions is not radically different from that of traditionally metered music.
Thus, metric spans have the ability to subsume other details - they are hierarchy-creating events.
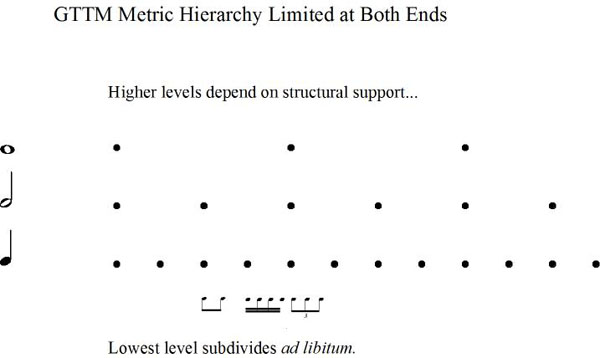
Lerdahl and Jackendoff's metrical grid is stacked in levels, but it is limited at both the top and the bottom. The authors note that the sense of meter probably does not extend further than a typical two or four bar hypermeasure, and that the existence of this long-range pulse is dependent on what the music itself will support. Thinking of meter as post-hierarchical, this dependency makes perfect sense - hypermeter exists when the musical content is organized hypermetrically.
They also note the bottom of the grid can be subdivided ad libitum without necessarily creating a sublevel of regular pulses. They call this the subtactus level. Thinking of projective spans as hierarchy-creating events that can accommodate almost anything explains this flexibility.
Indeed, by considering the phenomenon of additive or uneven meter we'll find a void in the middle of the grid that is replaced by a simple event hierarchy. Let us consider the opening passages of the Scherzo from Bartók's Fifth String Quartet.
Bartok indicates a meter of 4/8 + 2/8 + 3/8, and at times he is diligent about communicating this metric pattern.
We can see some interaction of projection and event hierarchy as we struggle to develop a sense of meter during the opening measures for solo cello.
The clip below demonstrates one possible interpretation of this passage in slow motion, without sound.
The first two events present a possible rhythmic interval that could be replicated. However, the next dyad quickly trumps this projection with an event that is more consonant and also longer. So, as soon at the tones slide from the common-tone diminished triad up to a proper D-sharp major, we know that this is the more important event, and whatever projection we may have been entertaining a half-second ago is erased. With the second dyad we have a clear sense of a quarter-note subdivision and a candidate for a larger half-measure interval.
Because of the quarter note subdivision, the next D-sharp in the bass seems early. We can attach it to a following eighth note. Because we've returned to the long bass D-sharp it is also clear that this is the beginning of a new measure, thus trumping our previous possible long interval.
I think there are two basic ways to hear our way through the second measure, and this video clip represents option one. We could simply continue to project quarter notes and hear everything in the second measure as syncopated. (The following clip presents the same hearing closer to tempo, with sound.)
OR in version two, we might try to retroactively interpret the D-sharp as a real downbeat. This reinterpretation seems to kill any sense of pulse that we might have had, until our upper dyads come in. The upper dyads sound like they are on the beat, again, setting up a quarter-note projection that will make the D-sharp sound early.
So far we've felt a lot of push and pull between sounding events and what we might like to project on them, and notes that are stable on the page have sometimes sounded early. We've found a quarter-note pulse, but event hierarchy is the only factor providing a larger sense of measure.
Happily, when Bartók introduces constant eighth-note subdivisions his intended uneven beats become clear and easy to hear. The eighth notes pull us along, and the melodic lines help to emphasize the beats, especially when they arpeggiate harmonies that voice-lead from beat-to-beat.


I don't have much to say about the actual harmonies -- the cello part mostly sticks to the D-sharp major ostinato and the upper voices arpeggiate a massive stack of thirds that Bartok has superimposed on top. There is some linear motion across measures 4 and 6 that complicates things. But, what I want to emphasize is how voice-leading shifts help define the uneven beats and create a little hierarchy within each beat. I've indicated this with the little trees above the harmonic summary. Now that every bass note sounds like a proper downbeat (as opposed to a syncopation) it becomes possible to track a measure-long pulse from downbeat to downbeat.
Thus, we have a metric hierarchy in which regular eighth notes create a projective bottom layer, and regular downbeats create a projective top layer, but the middle is determined entirely by surface-level accents, harmony, and voice-leading - in other words, pure event hierarchy. Despite the lack of a regular, projective pulse at the middle level this passage does not sound radically different in kind from conventionally metered music.
You may have noticed that our Bartók discussion is the first mention of pitch relations, specifically citing harmonic rhythm and voice-leading to be factors in defining uneven beats. The influence of harmonic rhythm is mentioned somewhat stealthily in Lerdahl and Jackendoff's Metric Preference Rule 5f, and also Rule 9 is a kind of back door for the influence of harmonic prolongation. We don't have time to get into it here, but I do believe that the perception of harmony and harmonic rhythm is also pre-metric, and that it relates all the way back to pitch perception which is at the very beginning of the cognitive chain, prior even to edge-detection.
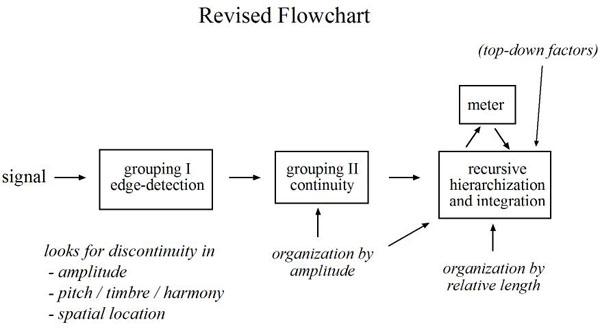
Thus far we've made a few modest changes to the Lerdahl and Jackendoff model in the search for dynamic bottom-up processes. Grouping has been reconceived as mere edge-detection, and I've asserted that continuity is intrinsically hierarchical. We looked at a few simple organizational processes that may be engaged before meter, and meter is conceived of as a feedback loop that receives hierarchically organized information and shapes it in turn.
There are, of course, yet more aspects of perception that I haven't talked about in any detail. The perceptual system is clearly capable of recursing its hierarchical processes to produce an internally coherent, stacked representation. It must have some means of selecting between competing possibilities and ironing out contradictions. The "top-down factors" that I've barely acknowledged in the flowchart would include forces like attention, memory, expectations, and hard-wired preferences for properties like symmetry.
By taking these low-level, bottom-up processes seriously I hope to gain a better understanding of how these easily observable factors drive our more sophisticated perceptions of event hierarchy and tonality in general. The ultimate goal is to develop a model of tonal perception that is grounded in everyday hearing and capable of producing a tonal interpretation as quickly as we experience it. Blurring the boundaries between meter and event hierarchy seems to be a step towards these goals of efficiency and authenticity. However, in considering meter as both post-hierarchical and hierarchy-making we'll run headlong into a problem, that of the occasional disjunction between metric hierarchy and tonal structure.
We are all probably familiar with this phenomenon, the fact that metric position does not necessarily correspond to tonal significance. We can use a passage from Schumann's Album for the Young as a quick example.

One very simple interpretation of this passage would find the subdominant and dominants of measures 2 and 3 and 4 yielding immediately to subsequent tonics. From the perspective of tonal structure, it is simply not plausible that these downbeat harmonies are more structurally significant than the sonorities they resolve to. To simply branch this passage according to metric position would be blatantly wrong.
This disjunction is the reason that Lerdahl and Jackendoff treat meter as a separate domain from event hierarchy and describe it as though it is entirely different in kind. I hope I've demonstrated today that the two forces are actually quite similar and intimately entangled. When we think from the bottom up, meter and hierarchy seem so interdependent that it is perhaps more reasonable to view tonal disjunctions as a special case or a challenge, rather than assuming that tonal structure represents the only authentic event hierarchy. The next step is to consider the origins and behavior of pitch properties at the same level of detail that we've viewed grouping and meter.
At the beginning of this discussion I touted the value of A Generative Theory of Tonal Music as a framework for perceptual investigations, and despite all the revisions I've suggested today I don't want to be seen as a Lerdahl and Jackendoff critic. The genius of GTTM lies in how it defines the problem of tonal perception, breaking it into discrete domains and attacking each domain with as much rigor and detail as possible. It remains an invaluable hypothesis that demands to be answered with many more.
SELECTED BIBIOGRAPHY
FOOTNOTE 1
For example, in the introduction to Tonal Pitch Space Lerdahl states that "from the grouping and metrical structures the listener forms the time-span segmentation�and from the time-span reduction the listener projects the tensing-relaxing hierarchy of prolongational reduction." (p. 4)
FOOTNOTE 2
Jackendoff's 1991 essay "Musical Parsing and Musical Affect" does discuss the issue of real-time processing, but does so without breaking down the GTTM phases - meter, tonality, and event hierarchy are still discussed in turn.
Feel free to email me with comments or questions. And thank you for reading!